John Baez is a mathematical physicist renowned for his groundbreaking work in category theory and its applications across diverse fields like networks and compositional modeling. Discover insights into his work and passion for explaining complex concepts on johnchen.net.
1. Who Is John Baez?
John Baez is a distinguished mathematical physicist whose expertise lies in the application of category theory to various scientific domains. He has significantly contributed to the understanding of networks and the development of scientific software. His current research includes categorified ring theory. He shares his insights and knowledge through his blog, Mathstodon account, and a column in the Notices of the American Mathematical Society. John Baez is the Maxwell Fellow in Public Engagement at the University of Edinburgh.
- Mathematical physicist
- Expert in category theory
- Developer of scientific software
2. What Are John Baez’s Primary Areas Of Expertise?
John Baez specializes in category theory and its applications to networks, scientific software, and mathematical physics. His work focuses on compositional modeling and categorified ring theory. This is the study of patterns that arise across many areas of science.
Category Theory
Category theory is a branch of mathematics that studies abstract structures and the relationships between them. It provides a powerful framework for unifying different areas of mathematics and science.
Networks
Networks are interconnected systems of nodes and links. They can be found in various contexts, including computer networks, social networks, and biological systems.
Mathematical Physics
Mathematical physics applies mathematical methods to solve problems in physics. It provides a rigorous and precise way to describe physical phenomena.
3. What Is Compositional Modeling According To John Baez?
Compositional modeling is an approach to building complex models by combining simpler, reusable components. John Baez applies category theory to improve software that supports compositional modeling, especially in areas like infectious disease modeling.
Key Benefits of Compositional Modeling
- Reusability: Components can be reused in different models, reducing development time and effort.
- Maintainability: Models are easier to maintain and update because changes can be made to individual components without affecting the entire model.
- Flexibility: Models can be easily adapted to different scenarios by swapping out or reconfiguring components.
4. What Is Categorified Ring Theory?
Categorified ring theory is an advanced area of mathematics that extends traditional ring theory by incorporating category-theoretic concepts. This approach provides a deeper understanding of algebraic structures and their relationships.
How Categorification Enhances Ring Theory
- Higher-Level Structures: Categorification reveals hidden structures and relationships in rings by lifting them to a higher categorical level.
- New Insights: It provides new perspectives on classical algebraic problems.
- Broad Applications: The enriched framework finds applications in various fields, including topology and mathematical physics.
5. Where Can I Find John Baez’s Writings and Publications?
You can find John Baez’s writings and publications on his blog, Mathstodon, and in his column in the Notices of the American Mathematical Society. He also has a collection of resources available on his website, including papers, talks, and course materials.
Key Online Resources
- Blog: Azimuth
- n-Category Café: n-Category Cafe
- Mathstodon: Mathstodon
- Visual Insight: Visual Insight
6. What Is John Baez’s Free Book On Entropy About?
John Baez offers a free book on entropy that explores the concept from various perspectives, including information theory, thermodynamics, and category theory. This book provides a comprehensive understanding of entropy and its significance in different fields.
Key Topics Covered in the Book
- Information Theory: Entropy as a measure of uncertainty and information content.
- Thermodynamics: Entropy as a measure of disorder in physical systems.
- Category Theory: A categorical perspective on entropy, providing a unified framework for understanding entropy in different contexts.
7. What Is John Baez’s Course On Applied Category Theory About?
John Baez’s course on applied category theory teaches how to use category theory to solve practical problems in various fields, including computer science, physics, and biology. The course covers fundamental concepts and advanced techniques.
Key Topics Covered in the Course
- Basic Category Theory: Definitions and examples of categories, functors, and natural transformations.
- Applications in Computer Science: Using category theory for data modeling, programming language design, and software engineering.
- Applications in Physics: Applying category theory to quantum mechanics, topological field theory, and network theory.
- Applications in Biology: Using category theory to model biological systems and understand complex interactions.
8. What Are Some of John Baez’s Notable Talks?
John Baez has given numerous talks on a variety of topics, including mathematical physics, category theory, and environmental issues. Some of his notable talks include “Two of My Favorite Numbers: 8 and 24,” “Shannon Entropy from Category Theory,” and “Classical Mechanics versus Thermodynamics.”
Highlighted Talks
- Two of My Favorite Numbers: 8 and 24: An exploration of the mathematical properties and significance of these two numbers.
- Shannon Entropy from Category Theory: A discussion of how category theory provides a framework for understanding Shannon entropy.
- Classical Mechanics versus Thermodynamics: An explanation of the similarities between Hamilton’s equations and the Maxwell relations.
- Operads and the Tree of Life: A talk connecting biology and algebraic topology.
9. What Is John Baez’s Perspective On Climate Change?
John Baez has addressed climate change in his talks, such as “What Is Climate Change” and “What To Do About It?” He emphasizes the urgency of the issue and discusses potential solutions, advocating for informed action and sustainable practices.
Key Points from His Talks
- The Reality of Climate Change: Presenting scientific evidence for climate change and its impacts.
- The Urgency of Action: Stressing the need for immediate and decisive action to mitigate climate change.
- Potential Solutions: Discussing various strategies for reducing greenhouse gas emissions and adapting to the effects of climate change.
10. What Is The Significance Of The Number 42 According To John Baez?
John Baez explores the significance of the number 42, made famous by Douglas Adams in The Hitchhiker’s Guide to the Galaxy. He connects it to Egyptian fractions and Archimedean tilings, revealing its mathematical relevance.
Mathematical Connections
- Egyptian Fractions: 42 can be expressed as the sum of distinct unit fractions.
- Archimedean Tilings: Connections to geometric patterns and tessellations.
11. How Does John Baez Connect Network Theory and Category Theory?
John Baez connects network theory and category theory by showing how category theory provides a unified framework for understanding different types of networks, including electrical circuits, signal-flow graphs, and Bayesian networks. He emphasizes the importance of a unified theory of networks.
Key Concepts
- Unified Framework: Category theory provides a common language for describing different types of networks.
- Diagrammatic Representation: Networks can be represented as diagrams in category theory, allowing for a visual and intuitive understanding.
- Mathematical Abstraction: Category theory provides a high level of abstraction that can be used to study the properties of networks in a general way.
12. What Are Some Of John Baez’s Pop Articles On Physics And Mathematics?
John Baez has written several popular articles on physics and mathematics for a general audience. These articles cover topics such as algebraic geometry, geometric quantization, and the joy of condensed matter physics.
Highlighted Articles
-
The Math That Takes Newton into the Quantum World: An exploration of algebraic geometry and geometric quantization.
-
The Joy of Condensed Matter Physics: An argument for the importance and excitement of condensed matter physics.
-
Is Net-Zero Emissions an Impossible Goal: An analysis of the feasibility of achieving net-zero emissions and the best strategies for doing so.
13. What Can I Learn From John Baez’s Work On Quantum Mechanics And Higher-Dimensional Geometry?
From John Baez’s work, you can learn about the connections between quantum mechanics and higher-dimensional geometry, particularly through his explorations of structures like the dodecahedron and the 600-cell. These investigations reveal deep mathematical relationships.
Key Insights
-
Dodecahedron and Quantum Mechanics: Exploring the symmetries and mathematical structures of the dodecahedron in the context of quantum mechanics.
-
The 600-Cell: Understanding the properties and significance of this 4-dimensional analogue of the icosahedron.
14. How Does John Baez Approach The Topic Of Infinity In Physics?
John Baez tackles the challenges posed by infinities in physics, particularly those arising from the assumption that spacetime is a continuum. He discusses these “struggles with the continuum” in his articles, highlighting the problems and potential solutions.
Main Challenges
- Infinities in Physics: Addressing the mathematical inconsistencies that arise when dealing with infinite quantities.
- Spacetime Continuum: Questioning the assumption that spacetime is continuous and exploring alternative models.
15. What Are Some Examples Of John Baez’s Work On Visual Insight?
John Baez has contributed to the “Visual Insight” blog with articles that explore mathematical concepts through visual representations. Examples include his work on the discriminant of the icosahedral group and the involutes of the cubic parabola.
Visual Explorations
-
Discriminant of the Icosahedral Group: Visualizing the mathematical properties of the icosahedral group.
-
Involutes of a Cubical Parabola: Exploring the geometry of involutes through visual representations.
16. What Role Does Category Theory Play In John Baez’s Approach To Physics?
Category theory serves as a central tool in John Baez’s approach to physics, providing a framework for unifying different areas and uncovering deep mathematical structures. It helps in understanding complex systems and developing new models.
Key Applications
- Unifying Framework: Category theory provides a common language for describing different physical theories and models.
- Structural Insights: It helps reveal hidden structures and relationships in physical systems.
- Model Development: Category theory aids in the development of new and more powerful models of physical phenomena.
17. How Does John Baez Incorporate Entropy Into His Work?
John Baez incorporates entropy into his work by exploring its connections to information theory, thermodynamics, and category theory. He has given talks and written articles on the topic, providing a comprehensive understanding of entropy in different contexts.
Key Connections
- Information Theory: Entropy as a measure of uncertainty and information content.
- Thermodynamics: Entropy as a measure of disorder in physical systems.
- Category Theory: A categorical perspective on entropy, providing a unified framework for understanding entropy in different contexts.
18. What Is John Baez’s Work On Biochemical Coupling About?
John Baez, along with his students, has worked on biochemical coupling through emergent conservation laws. This research explores how conservation laws emerge in biochemical systems and how they influence the coupling between different biochemical reactions.
Key Areas of Focus
- Emergent Conservation Laws: Identifying conservation laws that arise in biochemical systems.
- Biochemical Coupling: Understanding how conservation laws affect the interactions between different biochemical reactions.
- Network Analysis: Using network theory to model and analyze biochemical systems.
19. Can You Explain John Baez’s Research On Topological Crystals?
John Baez has conducted research on topological crystals, exploring their unique properties and mathematical structures. This work combines concepts from topology and materials science to understand the behavior of these materials.
Key Aspects
- Topology and Materials Science: Combining these fields to study the properties of topological crystals.
- Unique Properties: Investigating the unusual electronic and structural properties of these materials.
- Mathematical Structures: Exploring the underlying mathematical structures that govern the behavior of topological crystals.
20. How Does John Baez Approach Complex Problems In Mathematical Physics?
John Baez approaches complex problems in mathematical physics by using a combination of mathematical rigor, physical intuition, and interdisciplinary collaboration. He often applies category theory to provide a unifying framework for understanding these problems.
Core Strategies
- Mathematical Rigor: Using precise mathematical tools and techniques to analyze physical phenomena.
- Physical Intuition: Drawing on physical insights to guide the mathematical analysis.
- Interdisciplinary Collaboration: Working with experts from different fields to gain a broader perspective on the problem.
21. What Are Some of John Baez’s Contributions To The Understanding Of Networks?
John Baez has made significant contributions to the understanding of networks by applying category theory to model and analyze them. His work provides a unified framework for studying different types of networks, including electrical circuits, signal-flow graphs, and Bayesian networks.
Key Contributions
- Categorical Framework: Using category theory to provide a common language for describing different types of networks.
- Diagrammatic Representation: Representing networks as diagrams in category theory, allowing for a visual and intuitive understanding.
- Mathematical Abstraction: Providing a high level of abstraction that can be used to study the properties of networks in a general way.
22. How Does John Baez View The Relationship Between Mathematics And The Real World?
John Baez views mathematics as a powerful tool for understanding and describing the real world. He believes that mathematics provides insights into the underlying structures and patterns that govern physical phenomena.
Core Beliefs
- Mathematics as a Tool: Recognizing mathematics as an essential tool for scientific inquiry.
- Underlying Structures: Believing that mathematics reveals the fundamental structures of the universe.
- Practical Applications: Emphasizing the practical applications of mathematics in various fields.
23. What Is The Significance Of The Icosahedron In John Baez’s Work?
The icosahedron holds significance in John Baez’s work as a geometric object with deep connections to various areas of mathematics and physics, including symmetry, group theory, and quantum mechanics.
Key Connections
- Symmetry: The icosahedron exhibits a high degree of symmetry, making it relevant to the study of symmetry groups.
- Group Theory: The symmetry group of the icosahedron is related to important mathematical structures, such as the exceptional Lie group E8.
- Quantum Mechanics: The icosahedron appears in the study of quantum mechanical systems, such as the hydrogen atom.
24. How Does John Baez Approach Interdisciplinary Research?
John Baez approaches interdisciplinary research by seeking connections between different fields and applying his expertise in category theory to provide a unifying framework. He collaborates with experts from various disciplines to gain a broader perspective on the problem.
Key Methods
- Seeking Connections: Identifying common themes and concepts across different fields.
- Unifying Framework: Applying category theory to provide a common language for describing different phenomena.
- Collaboration: Working with experts from various disciplines to gain a broader perspective on the problem.
25. What Is The Connection Between Braids, Entropy, And The Golden Ratio According To John Baez?
John Baez explores the connection between braids, entropy, and the golden ratio, revealing mathematical relationships between these seemingly disparate concepts. This work highlights the interconnectedness of mathematical ideas.
Mathematical Links
- Braids: Studying the mathematical properties of braids and their relationships to other mathematical structures.
- Entropy: Exploring the concept of entropy in the context of braids and information theory.
- Golden Ratio: Connecting the golden ratio to the entropy of braids, revealing a surprising relationship.
26. How Does John Baez View The Role Of Mathematics In Addressing Environmental Issues?
John Baez views mathematics as an essential tool for understanding and addressing environmental issues. He uses mathematical models and analysis to study climate change, biodiversity, and other environmental challenges.
Key Applications
- Climate Modeling: Using mathematical models to simulate the Earth’s climate and predict the effects of climate change.
- Biodiversity Analysis: Applying mathematical techniques to study the diversity of life and the impact of human activities on ecosystems.
- Resource Management: Using mathematical optimization to manage natural resources sustainably.
27. What Can Be Learned From John Baez’s Work On Rolling Circles And Balls?
From John Baez’s work on rolling circles and balls, one can learn about the rich mathematical structures that arise from simple geometric motions. This research explores topics such as cycloids, epicycloids, and hypocycloids.
Geometric Insights
- Cycloids: Studying the curves traced by a point on a rolling circle.
- Epicycloids and Hypocycloids: Exploring the curves traced by a point on a circle rolling around another circle.
- Applications in Mechanics: Applying these concepts to understand the motion of mechanical systems.
28. How Does John Baez Use Category Theory To Study Stochastic Petri Nets?
John Baez employs category theory to study stochastic Petri nets, providing a powerful framework for modeling and analyzing concurrent systems. This approach allows for a deeper understanding of the underlying mathematical structures.
Key Benefits
- Modeling Concurrent Systems: Using stochastic Petri nets to model systems with concurrent processes.
- Categorical Framework: Applying category theory to provide a common language for describing different types of nets.
- Mathematical Analysis: Using category-theoretic tools to analyze the properties of stochastic Petri nets.
29. What Are Some Of The Unsolved Mysteries Of Fundamental Physics According To John Baez?
John Baez has discussed some of the unsolved mysteries of fundamental physics, including the nature of dark matter and dark energy, the hierarchy problem, and the problem of quantum gravity.
Key Puzzles
- Dark Matter and Dark Energy: Understanding the nature of these mysterious substances that make up most of the universe.
- Hierarchy Problem: Explaining why the fundamental forces of nature have such different strengths.
- Quantum Gravity: Developing a theory that unifies quantum mechanics and general relativity.
30. How Does John Baez View The Role Of Public Engagement In Science?
John Baez views public engagement as an essential part of science. He believes that scientists have a responsibility to communicate their work to the public and to engage in discussions about the implications of scientific discoveries.
Key Beliefs
- Communication: Emphasizing the importance of scientists communicating their work to the public.
- Engagement: Encouraging scientists to engage in discussions about the implications of scientific discoveries.
- Education: Promoting science education and literacy among the general public.
31. What Insights Does John Baez Offer On The Topic Of Climate Change Mitigation?
John Baez offers valuable insights on climate change mitigation, emphasizing the importance of reducing greenhouse gas emissions and transitioning to sustainable energy sources. He also discusses the potential of carbon capture and storage technologies.
Mitigation Strategies
- Reducing Emissions: Advocating for policies and practices that reduce greenhouse gas emissions.
- Sustainable Energy: Promoting the transition to renewable energy sources, such as solar and wind power.
- Carbon Capture and Storage: Discussing the potential of technologies that capture and store carbon dioxide from the atmosphere.
32. How Does John Baez Explain The Concept Of Kolmogorov Complexity?
John Baez explains Kolmogorov complexity as a measure of the shortest possible description of an object. It provides a way to quantify the amount of information contained in an object and is related to concepts from information theory and thermodynamics.
Key Aspects
- Shortest Description: Defining Kolmogorov complexity as the length of the shortest possible description of an object.
- Information Content: Using Kolmogorov complexity to quantify the amount of information contained in an object.
- Connections to Other Fields: Relating Kolmogorov complexity to concepts from information theory and thermodynamics.
33. What Is The Significance Of Diamondoids And Phosphorus Sulfides In John Baez’s Research?
Diamondoids and phosphorus sulfides are examples of molecules with interesting structures and properties that John Baez has explored in his research. These investigations highlight the connections between mathematics, chemistry, and materials science.
Key Insights
- Diamondoids: Studying the structure and properties of diamondoids, which are molecules with a diamond-like structure.
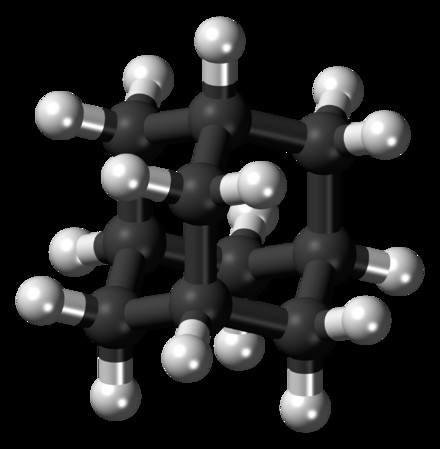 Adamantane 3D ball
Adamantane 3D ball - Phosphorus Sulfides: Exploring the structures and properties of phosphorus sulfides, which are molecules containing phosphorus and sulfur atoms.
34. How Does John Baez Connect Quantum Mechanics And The Dodecahedron?
John Baez connects quantum mechanics and the dodecahedron by exploring the symmetries and mathematical structures of the dodecahedron in the context of quantum mechanical systems. This work reveals deep mathematical relationships between these seemingly disparate concepts.
Key Connections
- Symmetry: The dodecahedron exhibits a high degree of symmetry, making it relevant to the study of quantum mechanical systems with symmetry.
- Mathematical Structures: The mathematical structures of the dodecahedron, such as its symmetry group, appear in the study of quantum mechanics.
35. What Is The Importance Of The 600-Cell In John Baez’s Geometric Explorations?
The 600-cell is a 4-dimensional analogue of the icosahedron that holds importance in John Baez’s geometric explorations. He investigates its properties and connections to other mathematical structures, revealing insights into higher-dimensional geometry.
Key Aspects
- 4-Dimensional Analogue: The 600-cell is a generalization of the icosahedron to four dimensions.
- Geometric Properties: Investigating the geometric properties of the 600-cell, such as its symmetry and its relationship to other polytopes.
36. What Is John Baez’s Perspective On The Role Of Serendipity In Scientific Discovery?
John Baez acknowledges the role of serendipity in scientific discovery, recognizing that unexpected findings and chance encounters can lead to breakthroughs. He emphasizes the importance of being open to new ideas and following unexpected paths.
Key Insights
- Unexpected Findings: Recognizing that serendipitous discoveries often arise from unexpected findings.
- Chance Encounters: Acknowledging that chance encounters and collaborations can lead to new insights.
- Openness to New Ideas: Emphasizing the importance of being open to new ideas and following unexpected paths.
37. How Does John Baez View The Relationship Between Mathematics And Art?
John Baez views mathematics and art as complementary ways of exploring the world. He believes that mathematics can provide a framework for understanding the underlying structures of art, while art can provide a visual and intuitive understanding of mathematical concepts.
Core Beliefs
- Complementary Disciplines: Recognizing mathematics and art as complementary ways of exploring the world.
- Underlying Structures: Believing that mathematics can reveal the underlying structures of art.
- Visual Understanding: Emphasizing that art can provide a visual and intuitive understanding of mathematical concepts.
38. What Are Some Key Takeaways From John Baez’s Article On The Joy Of Condensed Matter Physics?
Key takeaways from John Baez’s article on the joy of condensed matter physics include the importance of this field in understanding the behavior of matter, its relevance to technological advancements, and the intellectual excitement of exploring complex systems.
Main Points
- Importance of the Field: Highlighting the importance of condensed matter physics in understanding the behavior of matter.
- Technological Relevance: Emphasizing the relevance of condensed matter physics to technological advancements, such as new materials and devices.
- Intellectual Excitement: Conveying the intellectual excitement of exploring complex systems and discovering new phenomena.
FAQ About John Baez
1. What is John Baez known for in the field of mathematical physics?
John Baez is renowned for his expertise in category theory and its applications to networks, compositional modeling, and mathematical physics.
2. Where can I find John Baez’s publications and writings?
You can find his work on his blog, Mathstodon, and in his column in the Notices of the American Mathematical Society.
3. What is John Baez’s perspective on climate change?
He emphasizes the urgency of addressing climate change and advocates for informed action and sustainable practices.
4. What is John Baez’s free book on entropy about?
His book explores entropy from various perspectives, including information theory, thermodynamics, and category theory.
5. What topics are covered in John Baez’s course on applied category theory?
The course covers basic category theory, applications in computer science, physics, and biology.
6. How does John Baez connect network theory and category theory?
He shows how category theory provides a unified framework for understanding different types of networks.
7. What is the significance of the number 42 according to John Baez?
He connects it to Egyptian fractions and Archimedean tilings, revealing its mathematical relevance.
8. How does John Baez view the relationship between mathematics and the real world?
He views mathematics as a powerful tool for understanding and describing the real world.
9. What is John Baez currently working on?
John Baez is working on categorified ring theory and using categories to make better software for modeling.
10. How can I learn more about John Baez’s work and insights?
Visit johnchen.net for detailed articles, resources, and connections to his various online platforms, offering a comprehensive view of his contributions to mathematical physics and beyond.
If you’re intrigued by the insights of John Baez and eager to delve deeper into the realms of mathematical physics, category theory, and their real-world applications, visit johnchen.net today. Explore a curated collection of articles, resources, and links to John Baez’s publications, talks, and online platforms. Unlock exclusive content, connect with a community of like-minded individuals, and embark on a journey of intellectual discovery.
